|
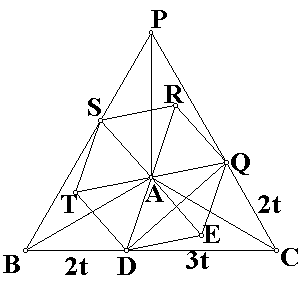
Reproduce two other congruent figures. Since ÐBAC = 120° and AB = AC , the 3 congruent figures can be jointed together to form a big equilateral triangle DPBC as shown in the right (with A as centre). Let ÐCAE = x, ÐBAC = 120°, ÐDAE = 60°, ÐBAD = 60° – x . So, by the property of congruent figures, ÐQAC = 60° – x , ÐQAE = 60° – x + x = 60° DAEQ is also an equilateral triangle Similarly, DAQR , DARS , DAST , DATD are equilateral triangles. They form a regular hexagon with A as centre. Let BD = 2t, CD = 3t, then CQ = 2t , ÐDCQ = 60° Area of DPBC = 3´50 cm2 = 150 cm2
Join DQ. Area of DADE = Area of DADQ Area of DDQS = Area of DPBC – 3× Area of DCDQ LLL (1)
|
 |