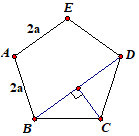
We find the length of the diagonal first.

ÐBCD = 108°

BD = 2´2a sin 54° = 4a cos 36°

Let q = 36°; 5q = 180; 3q = 180° – 2q

cos 3q = cos(180° – 2q)

4 cos³ q – 3 cos q = – cos 2q = 1 – 2 cos² q

4 cos³ q + 2 cos² q – 3 cos q – 1 = 0

(cos q + 1)(4 cos² q – 2cos q – 1) = 0

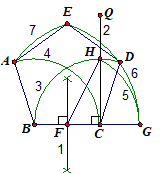
Steps:

1. Locate the mid-point F of BC.

2. Through C, draw a line CH perpendicular to BC.

3. Use C as centre, BC as radius to draw an arc BHD, cutting the line CH at H. Join FH.

    By Pythagoras' theorem on ΔCFH, FH =

4. Use B as centre, BC as radius to draw an arc AC.

5. Use F as centre, FH as radius to draw an arc GH, cutting BC produced at G.

6. Use B as centre, BG as radius to draw an arc EDG, cutting the arc BHD at D.

    BG is the length of diagonal of the pentagon.

7. Use C as centre, BG as radius to draw an arc AE, cutting the arc in step 4 at A, and also cutting the arc in step 6 at E. Join ABCDE.

This is the required regular pentagon.